Na ostatnich stronach rozporządzenia MNiSW o kategoryzacji jednostek naukowych opisana jest, przyjęta przez KEJN jako narzędzie klasyfikacji instytucji, metoda porównań parami. W majowym numerze „Forum Akademickiego” (nr 5/2012) jeden z nas naszkicował jej zarys i wskazał na powszechną, chociaż najczęściej nieświadomą, stosowalność. W tym artykule nie będziemy argumentować, dlaczego warto wprowadzić metodę porównań parami, poświęcając się (a raczej miejsce w FA i czas Czytelników) odpowiedzi na pytanie, jak wprowadzić ją w życie. Zdajemy sobie sprawę, że wszelkie próby tłumaczenia wzorów mogą i muszą (naprawdę muszą?) napotkać na poważny opór części odbiorców, ale obiecujemy dołożyć starań, aby chcących zrozumieć nie zniechęcić.

Przypomnijmy – każda jednostka naukowa oceniana jest według czterech kryteriów (aktywność naukowa i twórcza jednostki, jej potencjał naukowy, efekty materialne działalności naukowej, pozostałe efekty działalności naukowej), za które przyznawane są punkty. W kontekście procedury kategoryzacji te cztery wartości liczbowe stanowią zupełną charakterystykę jednostki. Należy też pamiętać, że skala punktacji każdego kryterium jest różna, a więc nie można ich porównywać: 50 punktów za aktywność naukową i twórczą (publikacje, patenty etc.) nie oznacza tego samego, co 50 punktów za potencjał naukowy. Zgodnie z notacją stosowaną w rozporządzeniu, ocenę (liczbę punktów) jednostki X względem kryterium „i” (i = 1, 2, 3, 4) oznaczamy Oi(X). Oceny są tak skonstruowane, że ich wyższa wartość odzwierciedla lepszą jakość efektów działalności jednostki. Ważnym aspektem jest to, że oceniamy wspólnie tylko pewną grupę jednostek o określonym charakterze działalności i określonych polach działania; nazywamy ją grupą wspólnej oceny (GWO). Pierwszym zadaniem w procedurze oceny jest porównanie jednostek w ramach danej GWO i uszeregowanie ich pod względem jakości – na podstawie ocen uzyskanych względem wymienionych powyżej kryteriów. Stworzona tym sposobem lista jest tylko elementem pomocniczym w procesie kategoryzacji.

Relacja przewyższania

Na początek zastanówmy się, jak porównać ze sobą dwie jednostki, nazwijmy je X i Y. Która jest „lepsza”? Gdyby charakterystyka jednostki obejmowała tylko jedno kryterium, sytuacja byłaby banalna – im wyższa ocena, tym lepsza jednostka. Ale kryteriów jest więcej i należy wziąć je wszystkie pod uwagę. Tu niestety musimy się przyznać – to nie my wymyśliliśmy, jak je porównać. Nad tym zagadnieniem od kilkudziesięciu już lat głowią się naukowcy zajmujący się dziedziną badań zwaną ostatnio „naukami decyzyjnymi” (decisions sciences ). Zaproponowali oni wiele efektywnych, ale niestety czasem dość skomplikowanych, rozwiązań. Spośród nich KEJN przyjął, w dość prostej postaci, pewne standardowe, dobrze zbadane i powszechnie akceptowane metody analizy wielokryterialnej. O nich tu piszemy.

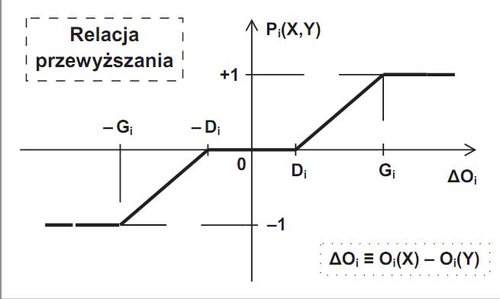
Po kolei. Weźmy pod rozwagę jedno z czterech kryteriów – „i” (i-te). W jego kontekście jednostki opisane są przez oceny Oi(X) oraz Oi(Y). Wynikiem porównania nie może być tylko stwierdzenie, która z tych dwóch liczb jest większa. Musimy różnicę „wycenić”. To zadanie realizujemy narzędziem zwanym relacją przewyższania. W definicji tej relacji (formalnie – funkcji, która różnicy Oi(X) – Oi(Y) przypisuje pewną wartość liczbową) bierzemy pod uwagę kilka aspektów. Nasze narzędzia oceniające nie są absolutnie doskonałe, więc mała różnica ocen nie wskazuje jednoznacznie, która jednostka przeważa. Definiujemy wobec tego próg nierozróżnialności, oznaczony Di, który wynosi (jak w rozporządzeniu) 10 proc. wartości oceny niższej z dwóch rozpatrywanych. Dla uproszczenia przyjmijmy, że Oi(X) ≥ Oi(Y) oraz oznaczmy symbolem ΔOi różnicę Oi(X) – Oi(Y), a symbolem Pi(X,Y) wynik przypisany jednostce X przy porównaniu jej z jednostką Y względem kryterium „i” (czyli wartość relacji przewyższania). Przy takich założeniach znaczenie progu nierozróżnialności Di jest następujące:

Di = 0,1•Oi(Y) ; jeśli ΔOi ≤ Di to Pi(X,Y) = 0.

Gdy ocena jednostki X jest znacznie większa niż ocena jednostki Y, to po przekroczeniu pewnej granicy, zwanej progiem pełnego przewyższania Gi, uznajemy, że przewaga jest całkowita. Nastąpił, według terminologii bokserskiej, nokaut. Dalsze zwiększenie różnicy punktowej nie skutkuje uzyskaniem większej liczby punktów w relacji przewyższania – nastąpiło „wysycenie” wartości tej funkcji. W rozporządzeniu przyjęto Gi = 3•Di. Działanie progu pełnego przewyższania zapiszemy jako warunek:

Gi = 3•Di (czyli Gi = 0,3•Oi(Y)) ; jeśli ΔOi ≥ Gi to Pi(X,Y) = 1.

W przypadku pośrednim (pomiędzy nierozróżnialnością a pełnym przewyższaniem) jednostka X uzyskuje liczbę punktów pomiędzy 0 a 1, proporcjonalną do różnicy ocen:

jeśli Di < ΔOi < Gi to Pi(X,Y) = (ΔOi – Di) / (Gi – Di).

Zależności te, uzupełnione o przypadek odwrotny (ocena jednostki Y jest wyższa, więc jednostka X przegrywa porównanie i uzyskuje punkty ujemne), pokazuje schematycznie załączony rysunek.

W najprostszym przypadku potrafilibyśmy już porównać ze sobą każde dwie jednostki X i Y. Używając opisanego powyżej mechanizmu relacji przewyższania stosowanego do ocen uzyskanych przez te jednostki w każdym z czterech kryteriów, uzyskamy cztery wyniki punktowe Pi(X,Y) dla jednostki X i analogiczne cztery wyniki Pi(Y,X) dla jednostki Y. Warto zauważyć, że relacja przewyższania spełnia warunek Pi(Y,X) = – Pi(X,Y), a więc nie musimy w praktyce porównywać Y z X (w takiej kolejności); wyniki dla jednostki Y w danym porównaniu otrzymujemy jako liczby przeciwne do wyników jednostki X. Wynikiem końcowym porównania X z Y byłaby suma czterech wyników punktowych: P1(Y,X) + P2(Y,X) + P3(Y,X) + P4(Y,X). Warto tu jeszcze raz podkreślić, że zastosowanie do porównywania ocen relacji przewyższania z osobna na każdym kryterium zapewnia ich całkowitą (matematyczną) niezależność. Porównywanych ocen Oi nie trzeba względnie normalizować, można wyrażać je w innych jednostkach – relacja przewyższania sprowadza, dla pary porównywanych jednostek, różnicę ich ocen do wartości punktowej z przedziału [–1,+1].

Cykl rozgrywek

Ze struktury sumy podanej pod koniec poprzedniego akapitu widać wyraźnie, że w takim uproszczeniu wszystkie kryteria traktujemy jako równo istotne. Tak jednak nie jest. Rodzaje, profile i zadania jednostek w kontekście składników poszczególnych kryteriów nie są takie same. Aby to zróżnicowanie oddać, KEJN posłużył się nieco bardziej złożonym schematem porównywania par jednostek – sumą ważoną relacji przewyższania. W zależności od rodzaju jednostek w danej GWO (wydziały uczelni, instytuty badawcze, jednostki PAN) oraz od ich przynależności do grupy dziedzin nauki, względne znaczenie poszczególnych kryteriów odzwierciedlane jest przez cztery wagi Wi. KEJN przyjął, że suma tych wag ma wynosić 100 (a więc można je traktować jako procentowy udział danego kryterium w końcowym wyniku porównania). Głównym składnikiem oceny jest kryterium aktywności naukowej i twórczej jednostki, a jego waga wynosi od 60 do 75 proc. (wyjątkiem są grupy wspólnej oceny obejmujące instytuty badawcze, dla których temu kryterium przyporządkowano wagę 35 proc.). Pozostałe kryteria ważą od 5 do 20 proc. Np. dla instytutów PAN w grupie nauk o życiu wagi kolejnych kryteriów to 75 proc., 5 proc., 10 proc. i 10 proc., natomiast instytuty badawcze w grupie nauk ścisłych i inżynierskich porównywane będą przy zastosowaniu wag wynoszących odpowiednio 35 proc., 10 proc., 45 proc. i 10 proc. Największe różnice występują dla kryteriów aktywności naukowej i twórczej jednostki oraz efektów materialnych działalności naukowej, gdyż odzwierciedlają one zadania i rolę każdego typu jednostek. Na zakończenie tej części podamy wzór na całkowity wynik punktowy V(X,Y) jednostki X w porównaniu jej z jednostką Y przy użyciu ważonej sumy relacji przewyższania:

V(X,Y) = W1•P1(X,Y) + W2•P2(X,Y) + W3•P3(X,Y) + W4•P4(X,Y).

Widać, że w porównaniu dwóch jednostek maksymalny możliwy do uzyskania wynik to 100 punktów (gdy we wszystkich kryteriach jednostka X w pełni przewyższa jednostkę Y, czyli Pi(X,Y) = +1 dla każdego i); oczywiście minimalny wynik to –100 punktów.

Aby uzyskać nasz pośredni cel uporządkowania jednostek w ramach danej GWO, dokonać należy „cyklu rozgrywek”, czyli wykonać porównanie każdej pary jednostek. Jeśli w danej grupie jest „m” jednostek, to każda z nich podlega m–1 porównaniom (nie ma sensu porównywać jednostki z samą sobą). W tych porównaniach każda jednostka wystąpi raz jako „X” (desygnat wyniku V(X,Y)), a raz jako „Y” (obiekt porównywany). Z każdego porównania jednostka Xk (k = 1, 2, ..., m) uzyskuje pewną liczbę punktów i jej „ostateczna ocena” OJN jest dana przez:

OJN(Xk) = [V(Xk,X1) + V(Xk,X2) + … + V(Xk,Xm)] / (m – 1),

przy czym w sumie (m–1) wyrazów w nawiasie kwadratowym nie występuje V(Xk,Xk). Mianownik jest wprowadzony tylko po to, by wyniki dla grup o różnej liczebności można było konfrontować (nie porównywać! różne GWO są z definicji niewspółmierne!). Wyniki OJN dla danej GWO można użyć do uszeregowania jednostek od najlepszej (największy wynik OJN) do najsłabszej.

Ważne: nie jest zamierzeniem KEJN stworzenie rankingu jednostek w każdej GWO! Zdajemy sobie sprawę (tu wyrażamy opinię całego Komitetu), że zastosowane elementy i metody oceny jakości działalności są zbyt mało precyzyjne, aby pokusić się o drobiazgowe rozróżnienia. Różnice kilku punktów w ostatecznym wyniku nie są na tyle znaczące, aby stwierdzić o przewadze jednej jednostki nad drugą. Ustawa nie wymaga tego – mamy „tylko” przyporządkować każdą jednostkę do jednej z trzech kategorii (A+ traktowane jest osobno). Łatwe byłoby podejście mechanistyczne: mamy ranking, wobec tego (to tylko przykład!) najlepsze 25 proc. wszystkich jednostek jest proponowane do kategorii A, ostatnie 10 proc. listy rankingowej do kategorii C, reszta w środku – do kategorii B. Schludne. I bardzo wątpliwe merytorycznie. Bo może wszystkie jednostki z tej GWO są bardzo dobre? A może tylko dobre i słabe, tak że żadna nie zasługuje na otrzymanie kategorii A?

Procedura kategoryzacji

Aby uniknąć powyższej słabości i odnieść przyznawane kategorie do standardów naukowych, KEJN zaproponował inne podejście. Dla każdej GWO z osobna zdefiniowane zostaną dwie modelowe jednostki referencyjne. Zdefiniowanie jednostki oznacza podanie wartości ocen w czterech kryteriach. Będą więc określone: jednostka referencyjna A, której oceny Oi(A) odpowiadają minimalnym wartościom ocen, jakich eksperci oczekują od jednostek kategorii A, oraz jednostka referencyjna B – analogiczne minimalne wartości oczekiwane od jednostki zaliczanej już do kategorii B. Nie mamy tu miejsca na opis, jak te wartości będą określane – eksperci bazować będą na swoim doświadczeniu w konkretnych obszarach nauki odnośnie do zwyczajów publikacyjnych; będą się też posiłkować statystycznymi analizami ocen jednostek w ramach GWO.

Procedura kategoryzacji będzie polegać na porównaniu wszystkich par jednostek w ramach GWO, z włączonymi modelowymi jednostkami referencyjnymi A i B (liczebność grupy „m” uwzględnia te dwie dodatkowe jednostki). W wyniku porównań przeprowadzonych w tak rozszerzonej GWO otrzymujemy wyniki OWJ, w tym także OWJ(A) i OWJ(B). Do kategorii A proponowane są wszystkie jednostki, których wynik OWJ jest nie gorszy od wyniku OWJ(A). Należy tu jednak podkreślić, że jednostka zaliczona do kategorii A nie musi mieć wszystkich ocen lepszych od ocen jednostki referencyjnej A. Z kolei te jednostki, których ostateczny wynik punktowy OWJ jest gorszy od OWJ(A), ale nie gorszy od OWJ(B), proponowane są do kategorii B. Jednostki, których ostateczny wynik z procedury porównań jest gorszy od OWJ(B), są kandydatami do otrzymania kategorii C. Ostateczne kategorie przydziela minister.

Autorzy tego opracowania zdają sobie sprawę, że nie udało się w tłumaczeniu uniknąć wzorów. Prosimy o wyrozumiałość – zgodnie z wytycznymi dawnych autorytetów staramy się przedstawić zagadnienie tak prosto, jak to jest możliwe, ale nie prościej. Mamy nadzieję, że matematyczne wzory nie przesłoniły zamysłu, a linia rozumowania była przystępna nawet dla zaprzysiężonego ideologicznie przeciwnika matematyki, dla którego fakt, że „zawsze w szkole miał z matmy pałę” jest powodem do chluby. Może motywacją do próby zrozumienia będzie sugestia, że aby móc podjąć krytykę, należy chociaż z grubsza wiedzieć, o czym mowa?