Pisanie o mechanice obliczeniowej – polu moich zainteresowań naukowych – w sposób zajmujący jest bardzo trudne. Można nawet zaryzykować twierdzenie, iż przedmioty techniczne z nim związane, wykładane na mojej Alma Mater, są jednymi z najbardziej nielubianych przez studentów. Jaka jest tego przyczyna? Nudne, niezrozumiałe, nieciekawe, trudne… A także niemające praktycznego zastosowania. Takie zarzuty padają najczęściej. O ile pierwsze określenia są z natury subiektywne, to z ostatnim oskarżeniem trudno się zgodzić. Student bowiem rzadko kiedy zdaje sobie sprawę, iż uruchamiając dowolny program obliczeniowy typu Robot czy Matlab (by wymienić te najczęściej używane) ma do czynienia z narzędziem zbudowanym na bazie szeregu modeli upraszczających skomplikowaną rzeczywistość inżynierską. Modele te mogą dotyczyć zarówno strony fizykalnej zjawiska, jak i opisu matematycznego. Jednakże najważniejszą rolę odgrywa numeryka , czyli techniki pozwalające na praktyczne („inżynierskie”) rozwiązanie zadania matematyki. Innymi słowy numeryka pozwala na otrzymanie w rezultacie liczby . Liczby mogącej wyrażać wartość przemieszczenia punktu konstrukcji, ale także określonej składowej naprężenia czy odkształcenia ciała. Bez odpowiedniej wiedzy, pozwalającej zrozumieć, skąd taka, a nie inna, wartość pojawia się „na wyjściu”, wynik bardzo trudno zinterpretować. Na poziomie studiów niezrozumienie może prowadzić do błędnie wykonanego projektu, w pracy zawodowej – nawet do katastrofy budowlanej.

Dalszą część artykułu pozwolę sobie zacząć anegdotą. Opowiadam ją zawsze studentom rozpoczynającym naukę metod numerycznych, przerażonym tym, co ich czeka w najbliższej przyszłości. Zapytano inżyniera, fizyka i matematyka, ile to jest „2+2”. Inżynier odpowiedział od razu, że „4”, fizyk po kilku godzinach pracy badawczej, iż „4.00001”, z dokładnością, co do wykonanego pomiaru i urządzenia pomiarowego. Natomiast matematyk… po dwóch miesiącach intensywnego wysiłku umysłowego stwierdził, iż wprawdzie rozwiązania nie znalazł, ale może udowodnić, że ono istnieje.

Anegdota niezwykle trafnie obrazuje sposób myślenia wymienionych specjalistów.

Kładka nad rzeczką

Każdy student, który poznał smak analizy matematycznej i algebry wykładanych na studiach, doskonale pamięta, jakiego szoku doznał na początku, będąc „jedynie” po kursie matematyki licealnej. W liceum bowiem matematyka sprowadzała się do opanowania w praktyce (tj. przy rozwiązywaniu zadań z treścią) kilku wzorów (w ramach określonej dziedziny). Na studiach wykłady z matematyki wyglądają nieco inaczej: stos pojęć pierwotnych, aksjomatów, definicji, założeń, twierdzeń i oczywiście dowodów tych twierdzeń. Matematyka „wykładowa” zdaje się mówić o wszystkim, tylko nie o tym, jak wiedzę w sposób praktyczny wykorzystać do rozwiązywania zadań. Dla przykładu, na polu równań różniczkowych (czyli równań, w których niewiadomą jest funkcja ukryta pod znakiem pochodnej), analiza matematyczna formułuje twierdzenia mówiące, czy rozwiązanie takiego równania istnieje (a jeśli istnieje, to kiedy) i czy jest jednoznaczne (tzn. czy jest ono jedyne, czy też może rozwiązaniem jest rodzina funkcji). Jednakże uzyskanie odpowiedzi na podstawowe pytanie: „jak wygląda to rozwiązanie”, jest możliwe tylko w przypadku niektórych prostych typów równań. Pół biedy, gdyby była to tylko abstrakcja, zupełnie nieprzydatna we współczesnej inżynierii. Ot, taka fanaberia matematyka – wymyśliłem równanie, teraz proszę mi to równanie rozwiązać… Tymczasem jest zupełnie odwrotnie: upraszczanie rzeczywistości poprzez budowanie rozmaitych modeli omawianego zjawiska prowadzi najczęściej do równań różniczkowych. Ich praktyczna analiza bez narzędzi numerycznych (czyli narzędzi pozwalających na ominięcie podejścia analitycznego, opartego jedynie na wiedzy teoretycznej o danym równaniu) byłaby niemożliwa. Z kolei nawet przy zastosowaniu odpowiednich technik obliczeniowych wykonanie tak wielu rachunków nie byłoby możliwe bez udziału komputera. I tu koło się zamyka.

W swojej pracy od samego początku zajmuję się rozwijaniem wybranych narzędzi numerycznych, służących do analizy tzw. problemów brzegowych . Matematycznie oznacza to właśnie potrzebę rozwiązania bardziej lub mniej skomplikowanego równania różniczkowego. Samo równanie jest najczęściej modelem matematycznym rzeczywistego zagadnienia inżynierskiego. Jakie to mogą być zagadnienia? Okazuje się, że codziennie się z nimi spotykamy, kiedy siedzimy, stoimy, jeździmy, pracujemy. Nasz ciężar jest bezpiecznie przenoszony przez mosty, kładki, płyty stropowe; możliwy jest bezpieczny przejazd przez wiadukt samochodem czy pociągiem. Mimo że są to ciała odkształcalne (tzn. doznają odkształcenia pod wpływem przyłożonego obciążenia), skutki tej deformacji są dla ludzi i samych konstrukcji na ogół nieodczuwalne. Zapewnia to odpowiedni dobór parametrów geometrycznych i materiałowych takich konstrukcji. Gwałtowny rozwój mechaniki obliczeniowej w ostatnich latach (idący za wzrostem prędkości obliczeniowej komputerów) pozwala na budowanie oraz analizę coraz to bardziej skomplikowanych modeli komputerowych konstrukcji, uwzględniających np. trwałe odkształcenia plastyczne (nieusuwalne po zdjęciu obciążenia z konstrukcji), lub też mechanizmy uszkodzenia i zniszczenia. Pozwala to przewidzieć czas bezpiecznej jej eksploatacji.

Jako przykład problemu brzegowego możemy sobie wyobrazić kładkę nad rzeczką, opartą na jej obydwu brzegach. Kładka ugnie się z chwilą, gdy zostanie obciążona. Relacja pomiędzy obciążeniem kładki a jej ugięciem to właśnie równanie różniczkowe. Sama kładka stanowi tzw. obszar zadania, a punkty jej podparcia – tzw. brzeg.

Funkcje węzłowe

Gdy zaczynałem pracę naukową, będąc jeszcze studentem III roku jednolitych studiów magisterskich, mój promotor zaproponował mi tematykę związaną z tzw. metodami bezsiatkowymi (ang. meshless methods ). W tym miejscu należy wspomnieć, iż do praktycznej analizy problemów brzegowych wykorzystuje się najczęściej tzw. metodę elementów skończonych (MES, ang. finite element method ), opracowaną w połowie XX wieku, stanowiącą podstawę 99 proc. dostępnego oprogramowania. Nieco na uboczu funkcjonowały inne alternatywne podejścia do MES, np. duża grupa metod zwanych bezsiatkowymi. Wywodzą się one z początku XX wieku, od metody różnic skończonych (MRS). Gwałtowny rozwój MES spowodował stagnację w rozwoju innych metod i dopiero teraz, gdy wszystkie dobrodziejstwa płynące z MES (oraz jej ograniczenia) są doskonale znane, sięga się po inne metody, być może bardziej efektywne i szybsze niż MES w niektórych zastosowaniach. Na ich autorach spoczywa obowiązek udowodnienia, iż warto w nie inwestować. Z metodami bezsiatkowymi, a zwłaszcza z najstarszą bezsiatkową metodą różnic skończonych (BMRS), sprawa jest nieco prostsza. To właśnie pracom polskim naukowców z lat 70. XX wieku zawdzięczamy rozwój metody (wtedy jeszcze pod nazwą – uogólniona MRS). Świat zainteresował się tymi metodami dopiero na początku lat 90. Od tego czasu na tym polu dzieje się naprawdę sporo.

Charakterystyczną cechą wszystkich metod komputerowej analizy problemów brzegowych jest to, iż dokonywana jest tzw. dyskretyzacja obszaru zadania. Oznacza to, iż zamiast szukać rozwiązania wszędzie (w całym obszarze), zakładamy jedynie skończony zbiór punktów (zwanych węzłami). W tych węzłach będziemy szukać wartości nieznanej funkcji. Wróćmy do poprzedniego przykładu kładki – jeżeli przyjmiemy jej model jednowymiarowy (kładka zamieni się w poziomą linię), to dyskretyzacja obszaru będzie polegała na wprowadzeniu zbioru węzłów w jednym poziomym kierunku. Przy czym warto wprowadzić węzeł na środku modelu kładki, bo tam najprawdopodobniej wystąpi jej największe ugięcie. W MES dyskretyzacja dokonywana jest za pomocą zarówno samych węzłów, jak i odcinków pomiędzywęzłowych (zwanych elementami skończonymi), razem stanowiącymi tzw. siatkę (ang. mesh ). Nieznanej funkcji, opisanej poprzez równanie różniczkowe, przyglądamy się zatem przez pryzmat elementu, pomiędzy węzłami. W MRS, BMRS i innych metodach bezsiatkowych wystarczą do tego celu same węzły . Ta cecha usprawiedliwia nazwę metod – bezsiatkowe: węzły są obecne, ale elementy nie są potrzebne, analiza funkcji dokonuje się dookoła węzłów.

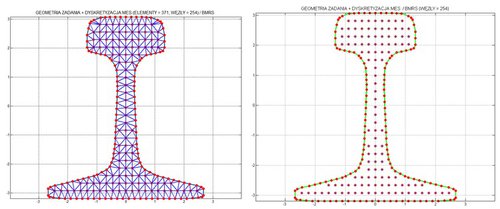
Jaką korzyścią charakteryzuje się takie postępowanie? Wszędzie tam, gdzie generacja siatki (węzły+elementy) jest uciążliwa lub gdy sama siatka musi ulegać ciągłym zmianom (np. wskutek niszczenia materiału), bardziej efektywne okazuje się korzystanie z metod bezsiatkowych. Różnicę w modelowaniu za pomocą MES i BMRS pokazuje rysunek 1 – przykład dyskretyzacji bardziej złożonego obszaru płaskiego – przekroju szyny kolejowej.

Siła metody

W swojej pracy zajmuję się głównie BMRS. Podstawy tej metody zostały opracowane już w latach 70. XX wieku. Mój wkład w metodę obejmuje przede wszystkim tzw. aproksymację podwyższonego rzędu, czyli takie sposoby opisu nieznanej funkcji, przy których końcowy wynik (wartości funkcji w węzłach) jest możliwie najlepszy przy stosunkowo małej liczbie węzłów. W dalszej kolejności zajmowałem się ulepszonymi metodami oceny błędu rozwiązania oraz taką przebudową położenia węzłów, aby ich końcowy układ możliwie dobrze oddawał cechy zadania. Warto nadmienić, iż zaproponowane przeze mnie i mojego promotora odpowiednie estymatory błędu (narzędzia do jego szacowania) należą do najnowocześniejszych na świecie. Wszystko to znalazło swoje pokrycie w szeregu przykładów i zastosowań z dziedziny mechaniki i inżynierii lądowej.

Jednakże przez czteroletni okres zbierania wyników do pracy doktorskiej nie bardzo wierzyłem, iż metoda, nad którą pracuję, znajdzie jakiekolwiek szersze zastosowanie. Dołączyłem do grupy osób, które jedynie w MES pokładały swoją ufność, co do jej olbrzymich możliwości i które wyrażały opinię, że zainteresowanie BRMS to tylko chwilowa moda. Jak bardzo się myliłem, udowodniły mi ostatnie lata, w których mogłem popatrzeć na swoje osiągnięcia z nieco innej perspektywy, z większym dystansem. Okazało się, iż nie jest tak źle. Na moją korzyść działał niejako brak dostępnego oprogramowania do BMRS i innych metod bezsiatkowych. Postanowiłem rozpropagować swoje własne autorskie programy w świecie, pisane jeszcze w czasach doktoratu, w cudownym środowisku graficzno-obliczeniowym Matlab, którego używam po dziś dzień. Muszę przyznać, że nie znalazłem niczego lepszego na swoje potrzeby. Oprogramowanie do BMRS rozrosło się do tak dużych rozmiarów, iż mogłem już stworzyć zamknięty program obliczeniowy, z graficznym interfejsem użytkownika i graficznym postprocesorem, który od dwóch lat służy w macierzystym instytucie zarówno do celów dydaktycznych, jak i naukowych. Program HeatMil pozwala na numeryczną analizę ustalonego i nieustalonego przepływu ciepła (to też przykład problemu brzegowego) za pomocą MES i BMRS. Rysunek 2 pokazuje przykładowy rozkład temperatury w szynie kolejowej, obliczony za pomocą BMRS.

Siłę opracowanego podejścia miałem możliwość przetestować w czasie praktyk zawodowych oraz innych programów stypendialnych i grantowych. Okazało się, że BMRS może znaleźć zastosowanie nawet w… projektowaniu systemu monitoringu istniejącej autostrady budowanej na terenach szkód górniczych Górnego Śląska oraz w systemach pomiarowych konstrukcji. Pierwszy z tych systemów został już wdrożony do użytkowania i doskonale spełnia swoją funkcję. Na rysunku 3 zaprezentowałem oszacowane rozpadlisko pod zakrzywionym odcinkiem autostrady, odtworzone na podstawie pomiarów wydłużeń krzyżujących się linek zamontowanych pod jej nawierzchnią.

W ostatnich latach miałem przyjemność opowiadać o metodach bezsiatkowych na rozmaitych kursach i szkoleniach organizowanych w ramach programów unijnych. Zainteresowanie, z jakim spotkały się te metody, upewniło mnie, iż warto było poświęcić kilka lat życia naukowego właśnie tej tematyce.